The Bernoulli Principle
Bernoulli’s theorem is the principle of energy conservation for ideal fluids in laminar, steady flow and has many engineering applications. In fluid dynamics, Bernouilli’s principle is the statement that:
"At points along a horizontal streamline, higher pressure regions have lower fluid speed and lower pressure regions have higher fluid speeds.”
This may sound counterintuitive to you since most people associate high speeds with high pressures, however we will explain below why this statement is indeed correct by applying Newton’s Second Law of motion to fluid within a tube.

Consider a horizontal water pipe which has a varying diameter – the first half of the pipe is wider than the second half of the pipe. Incompressible fluids that pass through the pipe will therefore have to speed up when they reach the narrower constricted section so that a constant volume flow rate is maintained. But where does this additional kinetic energy come from? As demonstrated by the work energy principle, the only way to give a fluid kinetic energy is do work on it, so there must be an external force acting on the fluid.
If we assume that the flow through the pipe is continuous and perfectly laminar, we will have no energy loss due to dissipative forces. It must consequently be non-dissipative forces that are doing work on the fluid causing it to speed up. In fact, it is the different surrounding fluid pressures in the narrow and wide sections of the pipe that result in a net force and thus accelerate the portion of fluid.
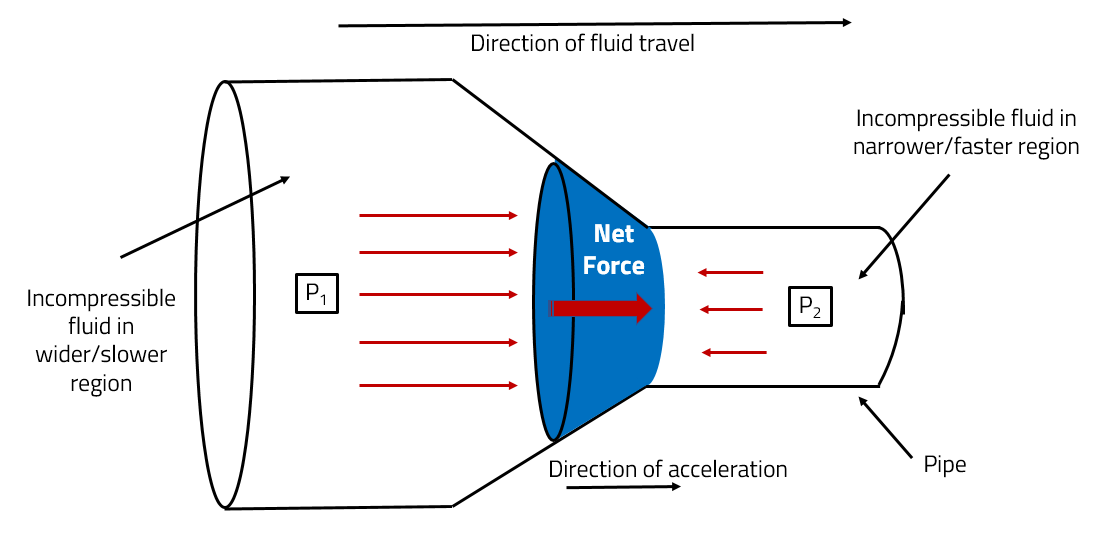
Consider the diagram above. As the fluid enters the narrower region, the force from pressure \(P_1\) pushes on the fluid in the direction of fluid travel and thus does positive work on the shaded section of the fluid. The force from pressure \(P_2\) pushes to the left and does negative work on the same portion of fluid, as it acts in the opposite direction to the motion of the fluid.
In accordance with the continuity equation, the shaded portion of fluid speeds up which means net positive work must be applied to it. Therefore, we can conclude the \(P_1 > P_2\) and qualitatively, that the wider and slower side of the tube has a lower pressure than the narrow and faster side. This inverse relationship between the speed and pressure at a point within a fluid is known as Bernoulli’s principle.
Bernouilli’s principle can be summarized concisely in one mathematical equation that also considers changes in gravitational potential energy:
where \(P\) is the pressure, \(\rho\) is the density of the fluid, \(v\) is the velocity of the fluid, \(h\) is the height of the fluid and \(g\) is the gravitational field constant. This equation is valid at any arbitrary point along a streamline, provided the flow is steady, incompressible, and that there is negligible friction from viscous forces.