Projectile Motion

Projectile motion is the free fall motion of an object in a horizontal path with constant velocity, as gravity is considered to be the only external force acting on it. The curved path along which the object consequently travels, is known as its trajectory. To predict the trajectory of a ball in flight, the initial velocity and position must be known to solve the kinematic equations . The velocity in the vertical and horizontal directions are as follows:

\(v_y = v sin\theta\)

\(v_x = v cos\theta\)

where \(\theta\) is the angle of projection measured upwards from the horizontal, \(v_x\) is the initial horizontal velocity, \(v_y\) is the initial vertical velocity.

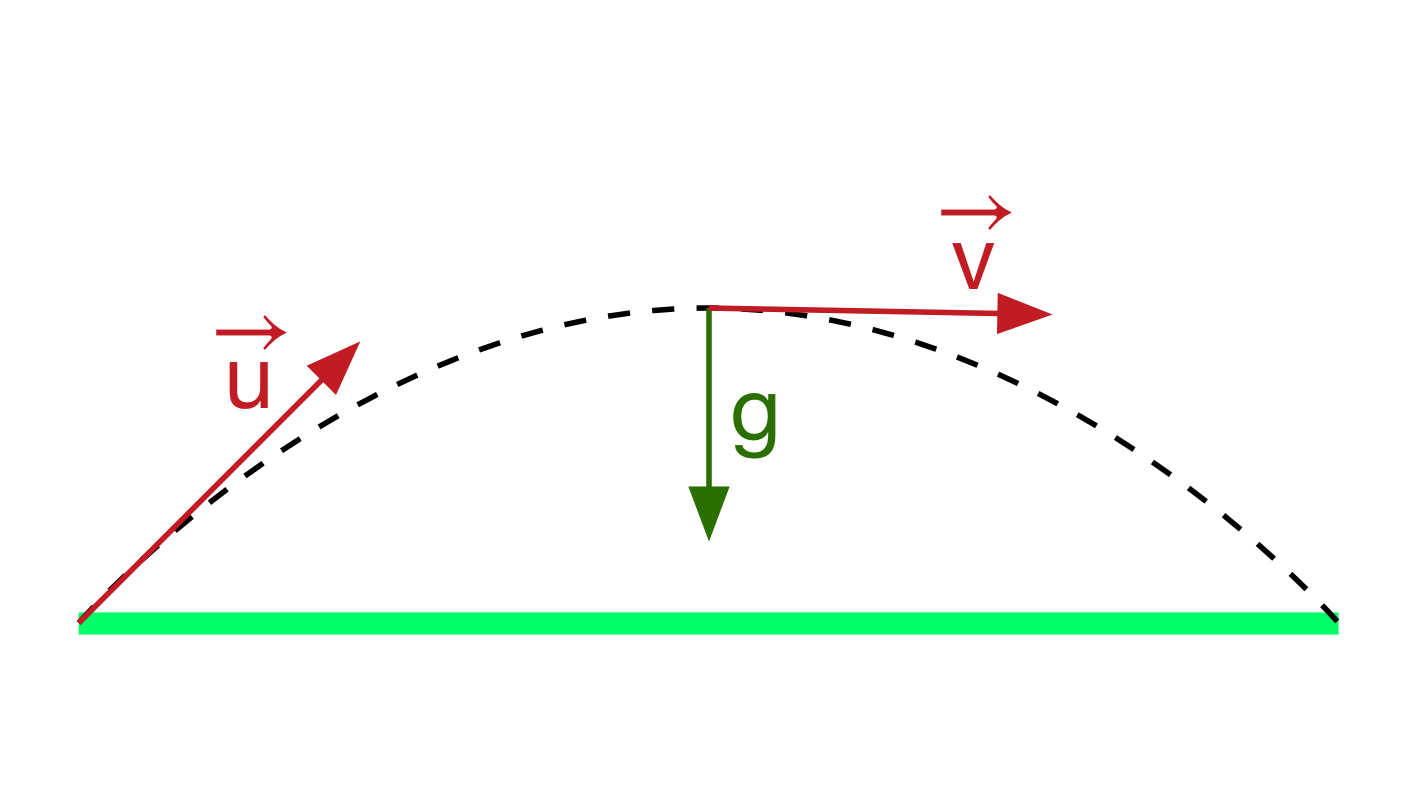
Below is a graphical representation of a simple ball trajectory under the sole influence of gravity:

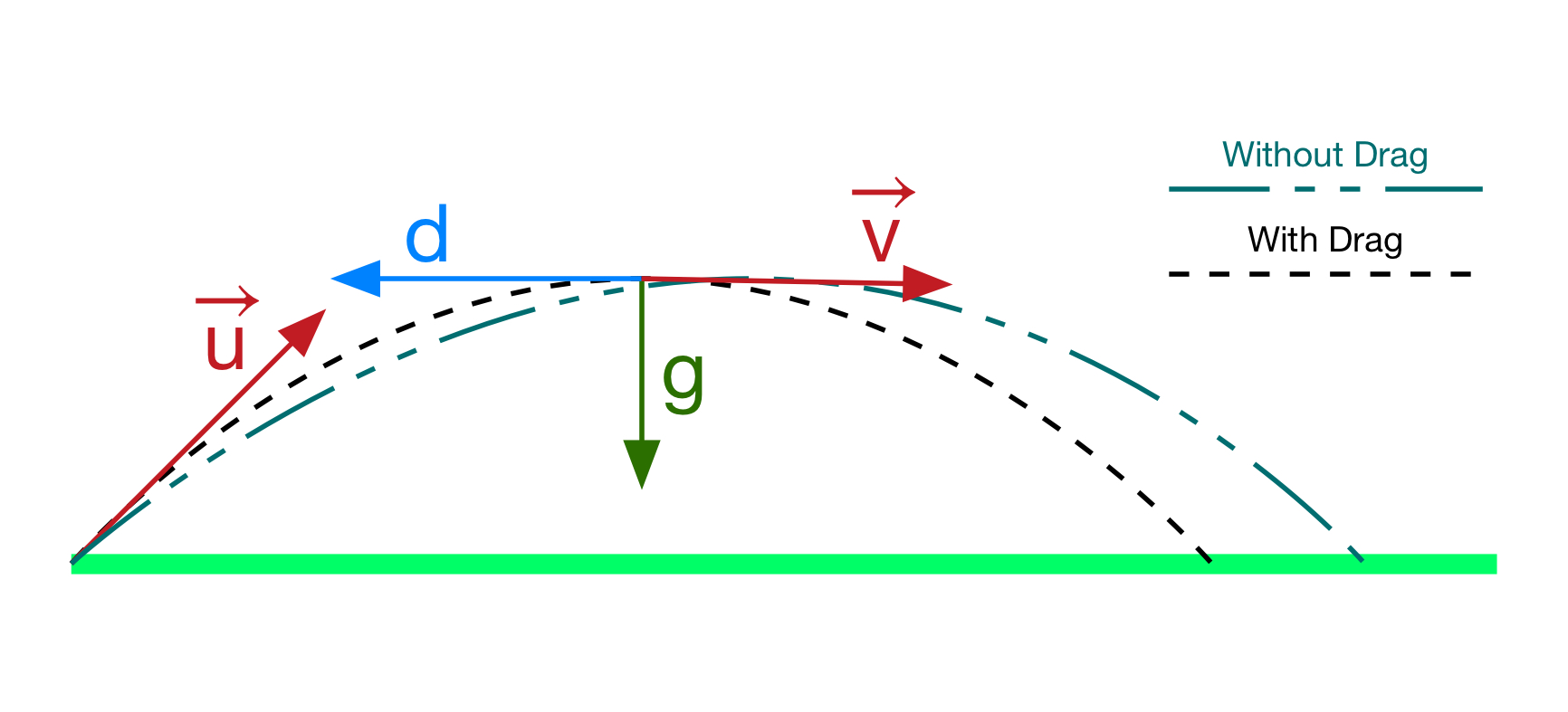
How to account for drag:

The model of a ball’s trajectory can be made more accurate with the inclusion of drag. In reality, due to the objects interaction with the medium it is travelling through, aerodynamic drag and lift forces also act on the ball when in flight. From Newton’s second law of motion in vector form we have that the net forces acting on the ball are:

\( \sum^t_0 F = m \frac{\partial^2x}{\partial t^2} \)

where \(F\) is the force acting on the body, \(m\) is the mass of the ball, \(t\) is the time and \(x\) is the position vector. As described on the sports pages, the drag forces on the ball are greatly impacted by the application of spin, therefore it is essential that we include this information. This is achieved by the inclusion of the drag coefficients, unique to each ball type and dependent on the Reynolds number.

Thus, in our advanced model we will include the following drag \(F_D\) and lift \(F_L\) forces along with gravity in the equation above to calculate the acceleration and therefore trajectory of the ball, where:

\( F_L = C_L \frac{1}{2} \rho A V^2 \)

\( F_D = C_D \frac{1}{2} \rho A V^2 \)

Here \(C_L\) and \(C_D\) are the lift and drag coefficients, \(\rho\) is the fluid density, an \(V\) is the velocity of the bulk fluid moving past the object. The area, \(A\), is calculated based on the forward projected area of the ball that is in a perpendicular direction of fluid flow.

How to solve the drag equation

The inclusion of drag means that we can no longer rely on the kinematic equations. Instead we use Newton’s equations of motion, which lead to first order non-linear differential equations that can then be solved to predict the ball’s trajectory . Assuming the ball has topspin, these can be written as follows:

\( m \frac{dv_x}{dt} = - F_d cos\theta + F_L sin\theta \)

\( m \frac{dv_y}{dt} = -F_d cos\theta - F_L sin \theta -mg \)

One can integrate the above equations to find the horizontal and vertical displacements of the ball provided the initial velocities and launch angles of the ball are known. From these calculations, it is easy to see the effect that spin and thus drag has on the trajectory of a ball if we compare it to the trajectory of a ball undergoing projectile motion. Below is a graphical illustration of the difference: