Laminar and Turbulent Airflow
Laminar Flow
Fluid flow in which the speed varies layer by layer is called Laminar or Streamline flow. In laminar flow, the velocity, pressure, and other flow properties remain constant at each point in the fluid.
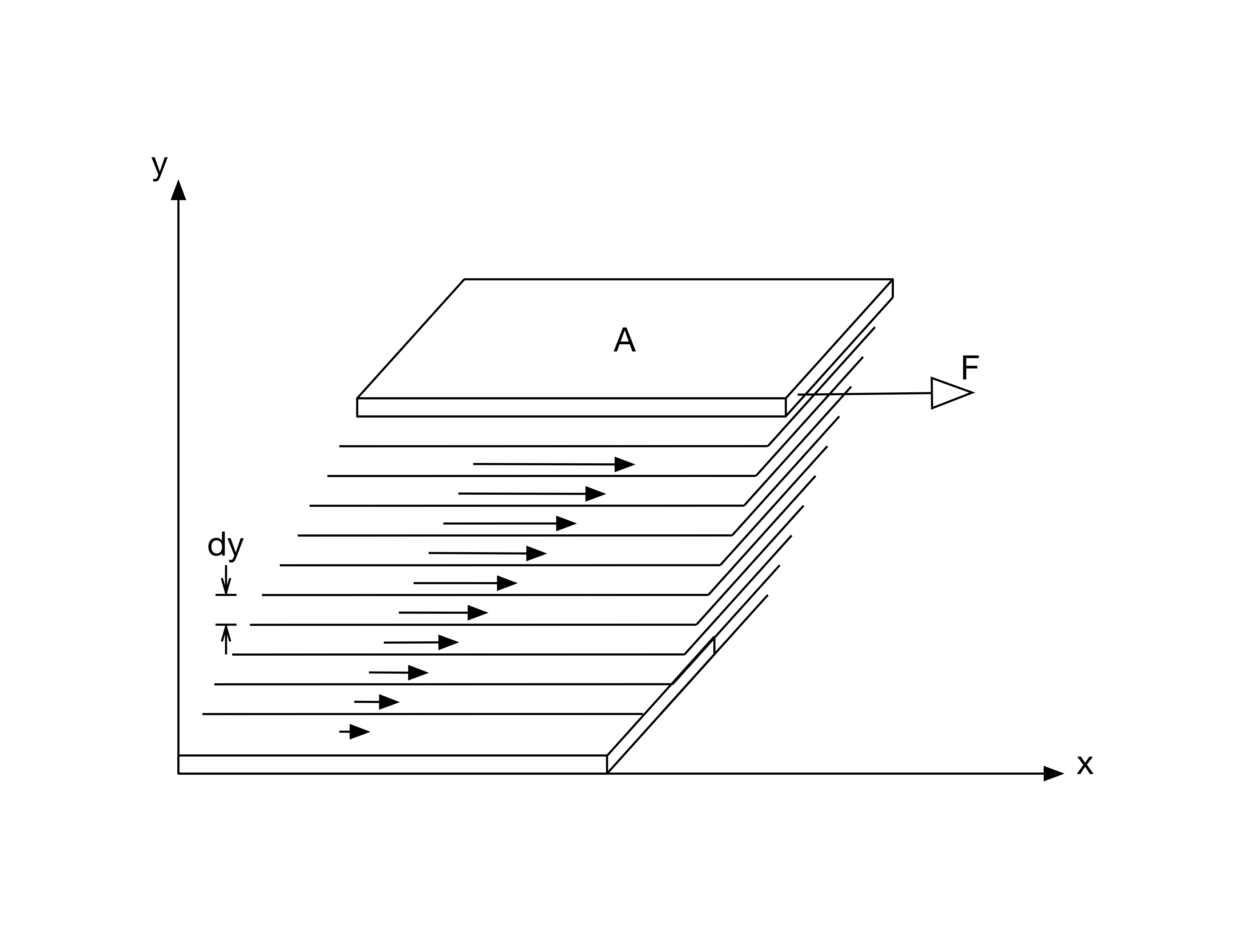
Laminar flow is observed in cases when the velocities are not high, the viscosity of the fluid is fairly high and the flow channel is relatively small. Laminar flow over a horizontal surface can be considered as parallel layers, or laminar sliding over one another, with the layer in contact with the horizontal surface being at rest while the velocity of all the other layers of fluid increases uniformly.
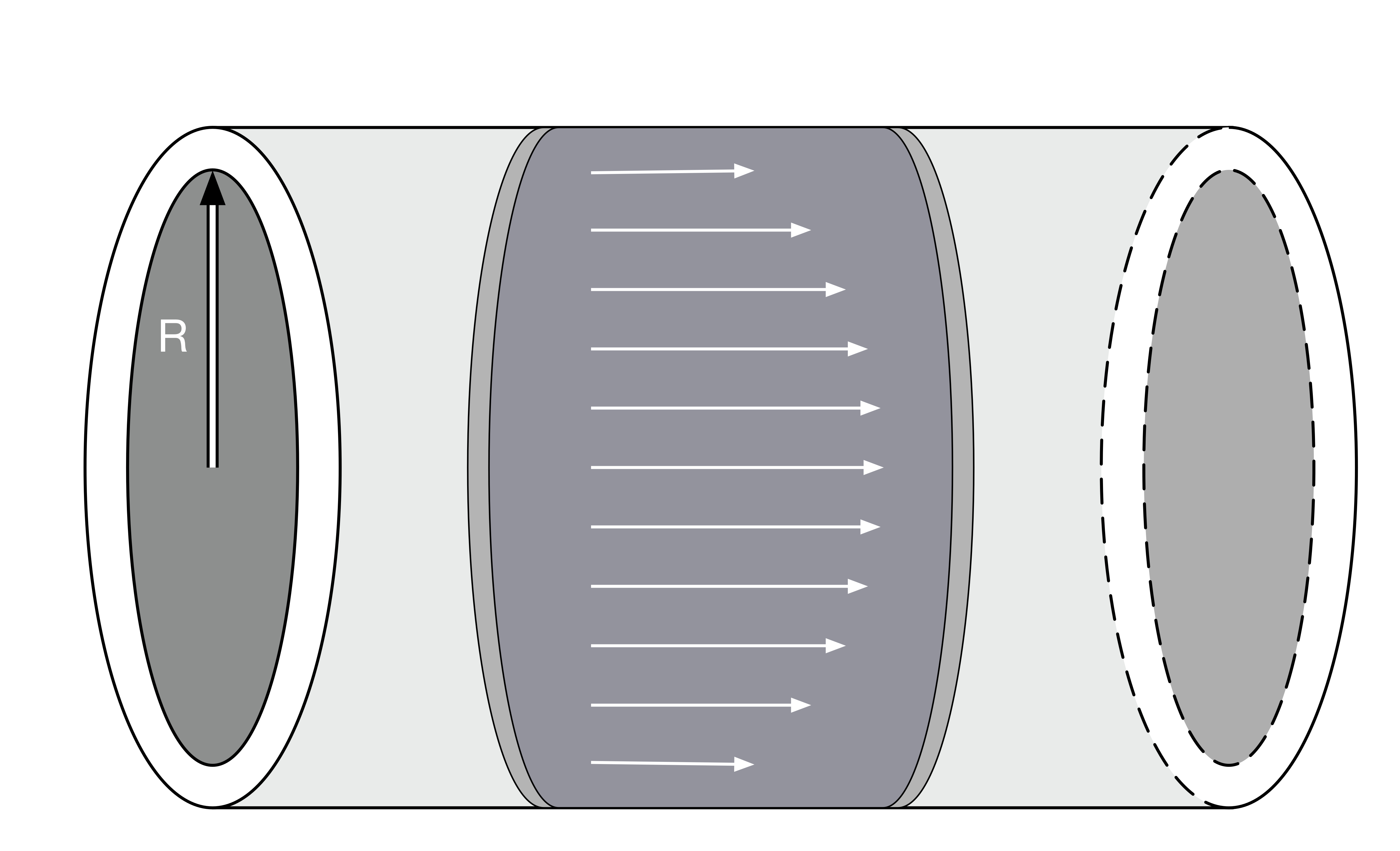
Laminar flow through a cylindrical pipe may be considered as concentric cylinders of fluid, with the outermost cylinder being at rest (due to contact with the surface of pipe) and the cylinder near the axis through the centre of the pipe having the highest velocity.
Turbulent Flow
Turbulent flow is a type of fluid flow in which the fluid undergoes irregular fluctuations, giving the flow irregular velocity components transverse to the flow direction. An example of this case is the flapping of a flag in breeze. If the air flow was laminar, the flag would occupy a fixed position along streamlines. However, since the flag pole acts as an obstacle in the laminar fluid flow, and thus breaks the flow into an irregular pattern causing turbulence, the flag seems to flap.
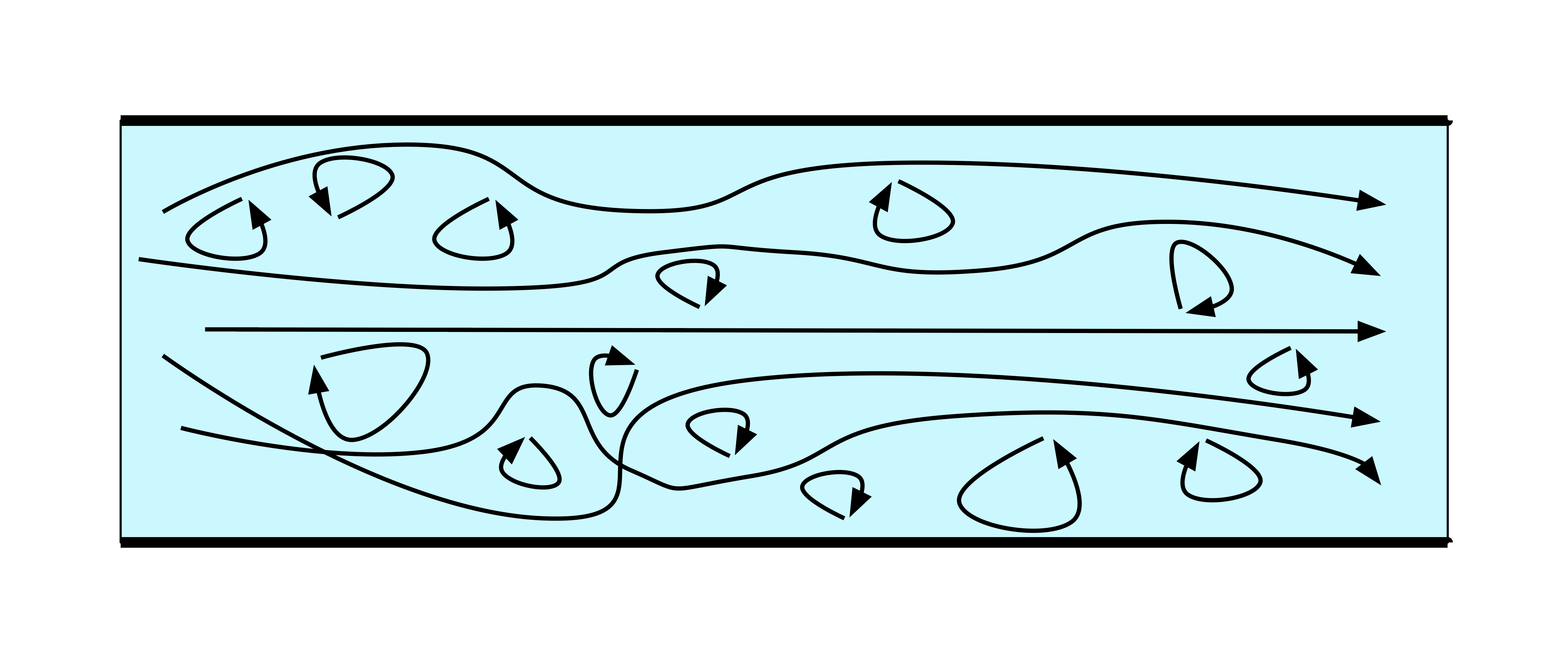
So long as the speed of a viscous fluid is low, and is unhindered, it can be considered as laminar flow. However, when the flow speed in a viscous fluid becomes sufficiently large, the motion becomes disordered and irregular. An analogy of this could be a block of stone being pushed across a surface. If the frictional force is small, the block will slide across the surface provided the applied force is at least as large as the frictional force. Whereas, if the frictional force is very large, the applied force must also be larger, therefore eventually causing the block to tip over. This tipping of the block could be considered as the transition from laminar flow to turbulent flow.

The critical speed at which the fluid flow becomes turbulent, for a cylindrical pipe, is given by:
where, \(\eta\) is the viscosity of the fluid, \(\rho\) is the density of the fluid and \(D\) is the diameter of the pipe. \(R\) is called the Reynold’s number, which is used to characterise any flow. We can experimentally determine the value of the Reynold’s number at which the flow becomes turbulent. it is a very useful concept, since it can predict when the flow will become turbulent in a particular case.