The Magnus Effect
The Magnus Effect is a physical phenomenon in which a lateral force is exerted on a symmetric object solely due to the rotational motion of the body. This lateral force is often thought of as a lift force which arises when the rotation of the body drags the fluid boundary layer in the same direction as the rotation, and thus modifies the pressure distribution and imparts a resultant force on the object. The effect is most commonly associated with the altered trajectories of spinning balls; tennis slices, swing bowling and golf hooks are all due to this phenomenon.
The Magnus force exerted on an object moving through a fluid can be caluated as :
\(F_M = C_L \frac{1}{2} \rho Av^2 \)
where \(C_L = \frac{C_M r \omega}{v} \) with \(\omega\) the rotational velocity of the ball, \(A\) the cross sectional area of the ball and \(C_M\) the coefficient of proportionality. In order to fully understand the Magnus effect, we will analyse its impact on the trajectory of a spinning ball.
First, we need to introduce an additional quantity into our description of a ball’s trajectory. The Reynolds number, defined as the relative magnitudes of viscous to inertial forces imposed on the object due to the flow field, can be written as follows:
\(Re = \frac{uD\rho}{\mu} \)
where \(u\) is the velocity of the object relative to the fluid, \(D\) is the diameter of the ball, \(\rho\) is fluid density and \(\mu\) is the dynamic viscosity of the fluid in the flow field.
In general for rough surfaces the layer can become turbulent when \(Re > 4 \times 10^4\). For smooth surfaces, the flow only transitions from laminar to turbulent when \(Re > 3 \times 10^5\). A negative Magnus effect occurs in the critical Reynolds region of around \(Re \approx 2 \times 10^5\) whereas, a positive Magnus force is induced when the boundary layer is either turbulent or laminar on both ball sides.
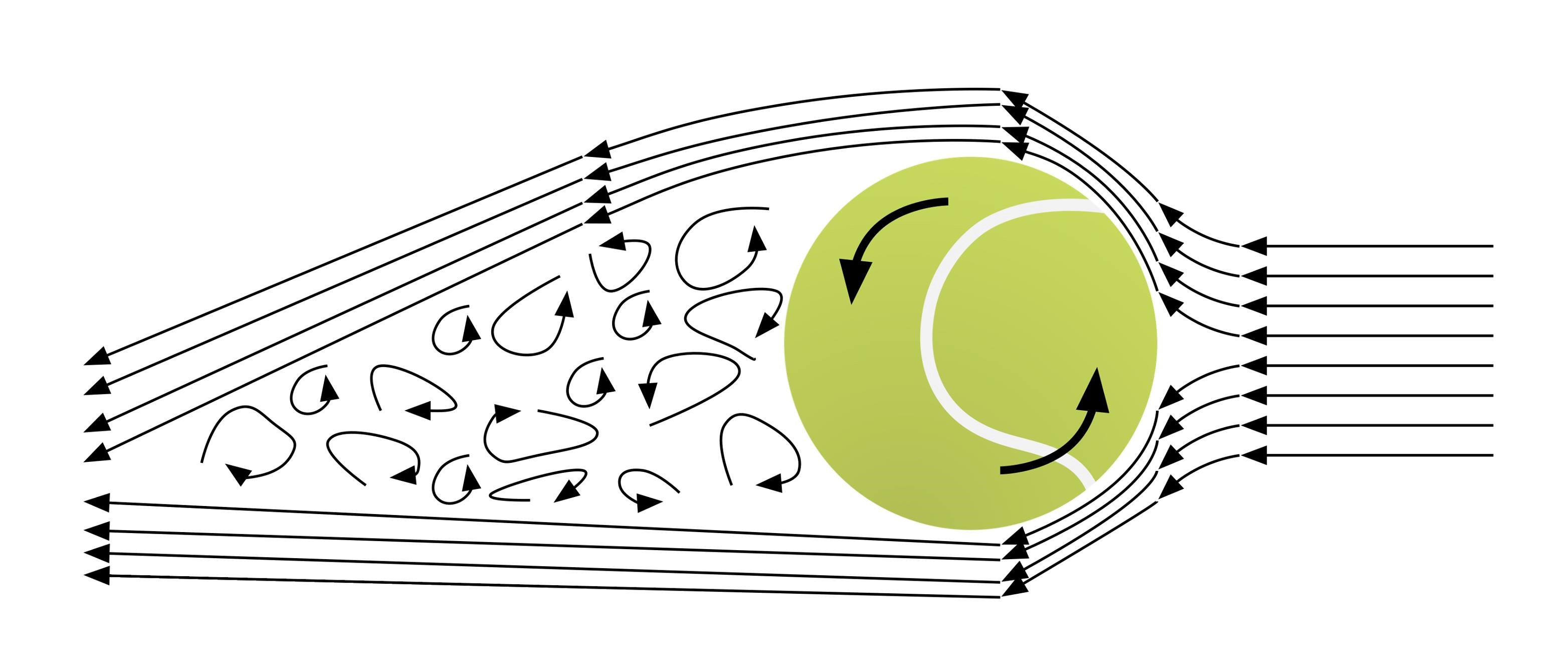
When clockwise rotation is imparted on a ball which is launched from left to right, the boundary layer on the upper side of the ball seperates earlier than at the bottom of the ball due to unequal drag forces acting on either end. As a result there is a pressure differential then causes an upward deflection of the wake behind the ball, and thus according to Newton’s Third Law of Motion, there is a downward force, known as the Magnus force, exerted on the ball. This resultant downward force consequently makes the ball fall to the ground at a faster rate than if spin had not been applied to the ball.
Similarly, if instead the ball had been spun in a counter-clockwise direction, there would have been a downwards deflection of the wake behind the ball which causes a subsequent upward Magnus force imparted on the ball. As a result, the spun ball would travel a larger horizontal distance than a nonspinning ball in this scenario.